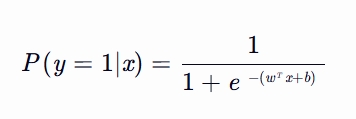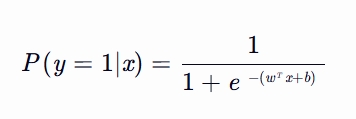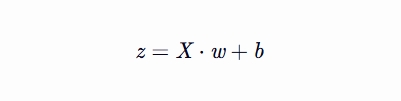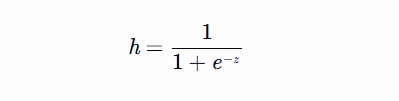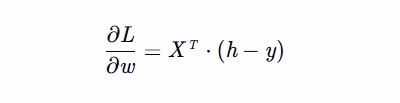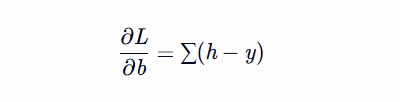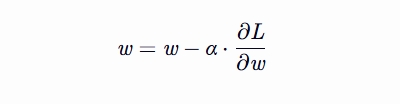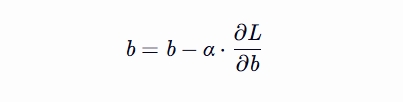1. 逻辑回归是一种用于处理二分类问题的监督学习算法, 逻辑回归=线性回归+sigmoid函数
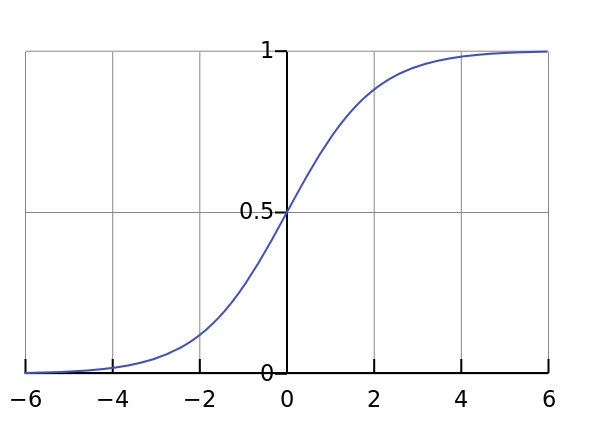
2. 逻辑回归核心思想是通过逻辑函数(Sigmoid函数)将线性回归的输出映射到(0,1)区间,从而得到样本属于某一类别的概率, Sigmoid函数之所以叫Sigmoid,是因为函数的图像很想一个字母S
3. 公式参数详解:
P(y=1∣x):这里的 x 代表样本的特征向量,包含了样本的各种属性或信息;
y 代表样本的类别标签,通常在二分类问题中取值为 0 或 1。P(y=1∣x) 就是在已知样本具有特征 x 的条件下,该样本属于类别 1 的概率
e:是一个精确的常数,近似值:e≈2.718281828459045…(无限不循环小数)
w:是权重向量,表示各个特征对结果的影响程度,特征的权重更大,表明它对预测结果的影响更大,也叫斜率
x:是特征向量,包含了样本的各种特征
b:是偏置项,用于调整决策边界的位置, 也叫截距
4. 机器学习工作流程
1.获取数据
2.数据基本处理
3.特征工程
4.机器学习(模型训练)
5.模型评估
结果达到要求,上线服务
没有达到要求,重新上面步骤
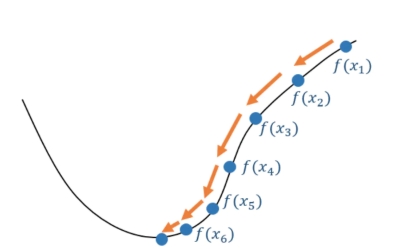
2. 使用梯度下降法找到最优的 w 和 b,使得模型预测的概率尽可能接近真实的类别标签 举例
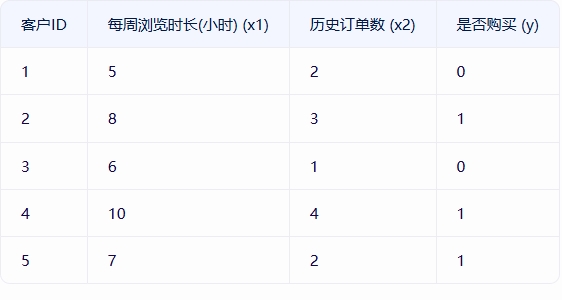
假设你是一家电商公司的数据分析师,想要预测客户是否会购买某款新产品(二分类问题:购买=1,不购买=0)
# Python代码实现示例
import numpy as np
# 训练数据 [每周浏览时长, 历史订单数]
X = np.array([[5, 2], [8, 3], [6, 1], [10, 4], [7, 2]])
# 是否购买
y = np.array([0, 1, 0, 1, 1])
# 初始化参数
w = np.array([0, 0])
b = 0
# 学习率: 可使用 网格搜索, 学习率衰减, 自适应学习率方法确定学习率, 大家可自行学习
alpha = 0.1
# 最大迭代次数设为 1000 次, 可以通过 损失曲线、交叉验证、早停法等手段优化迭代次数, 提前退出,, 大家可自行学习
max_iter = 1000
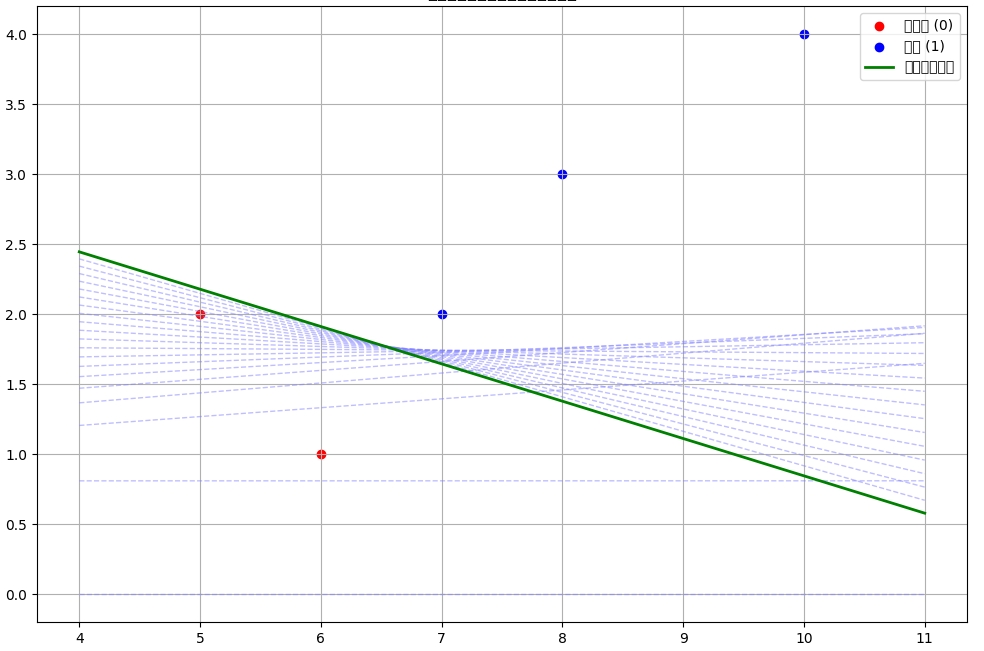
# 梯度下降最小化损失函数 w 和 b,从而确定决策边界
for _ in range(max_iter):
# 计算线性组合
z = np.dot(X, w) + b
# 计算预测概率
h = 1 / (1 + np.exp(-z))
# 计算梯度
dw = np.dot(X.T, (h - y)) / len(X) # /len(X) 损失函数对权重向量 w 的梯度
db = np.sum(h - y) / len(X) # /len(X) 损失函数对偏置项 b 的梯度
# 更新参数
w = w - alpha * dw
b = b - alpha * db
print("权重向量 w:", w)
print("偏置项 b:", b)
# 预测新数据
new_sample = np.array([9, 3])
z = np.dot(new_sample, w) + b
probability = 1 / (1 + np.exp(-z))
prediction = 1 if probability > 0.5 else 0
print(f"预测概率: {probability:.4f}")
print(f"预测类别: {prediction}")
计算线性组合
计算预测概率
计算梯度dw 损失函数对权重向量 w 的梯度
计算梯度db 损失函数对偏置项 b 的梯度
更新参数 更新权重向量 w
更新参数 更新偏置项 b
import numpy as np
from sklearn.linear_model import LogisticRegression
# 训练数据 [每周浏览时长, 历史订单数]
X = np.array([[5, 2], [8, 3], [6, 1], [10, 4], [7, 2]])
y = np.array([0, 1, 0, 1, 1])
# 初始化并训练逻辑回归模型
model = LogisticRegression()
model.fit(X, y)
# 输出训练后的参数
print("权重向量 w:", model.coef_[0]) # 注意:sklearn返回的权重是二维数组
print("偏置项 b:", model.intercept_[0])
# 预测新数据
new_sample = np.array([9, 3]).reshape(1, -1) # 需要reshape为二维数组
probability = model.predict_proba(new_sample)[0][1] # 获取类别1的概率
prediction = model.predict(new_sample)[0] # 直接预测类别
print(f"预测概率: {probability:.4f}")
print(f"预测类别: {prediction}")
逻辑回归作为二分类算法因其简单性、可解释性和高效性,仍是工业界和学术界的常用工具,尤其适合需要快速部署和解释的场景。